GAN개념과 DCGAN 구현

GAN 개념

생성적 적대 신경망(GAN)

GAN(Generative Adversarial Network)
기존 CNN은 가장 높은 probability 혹은 likelihood만 찾아 낼수 있었다.
GAN은 여기서 한발 더 나아가, '데이터의 형태' 를 만들어내고자 한다.
데이터의 형태라는 것은 분포 혹은 분산을 의미한다.

이미지의 형태를 예로 들어보자. 우리는 픽셀들의 분포에 따라 이 모양은 코, 이 모양은 눈이라는 것을 인식한다. (명암이나 사진의 전체적인 채도와는 큰 상관이 없다.)

분포를 만들어낸다는 것은, 단순히 결과값을 도출해내는 함수를 만드는 것을 넘어서 '실제적인 형태' 를 갖춘 데이터를 만들어낸다는 것이다.

적대적 생성

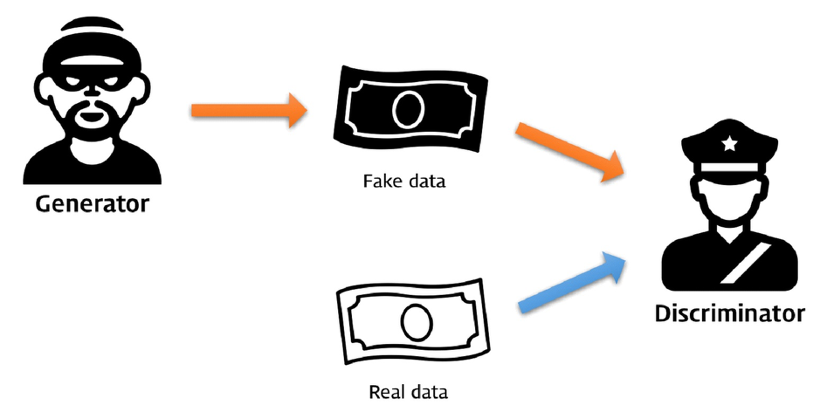
지폐 위조범에게 Generator라는 역할을 부여하자. 그리고 경찰은 Discriminator라는 역할을 부여한다.
위조범(Generator)은 경찰의 단속을 피하기 위해서 더욱 정교한 가짜 지폐를 만들어내고, 경찰(Discriminator)은 점점 더 정교한 기법으로 지폐를 판별해내는 방법을 개발해낸다.

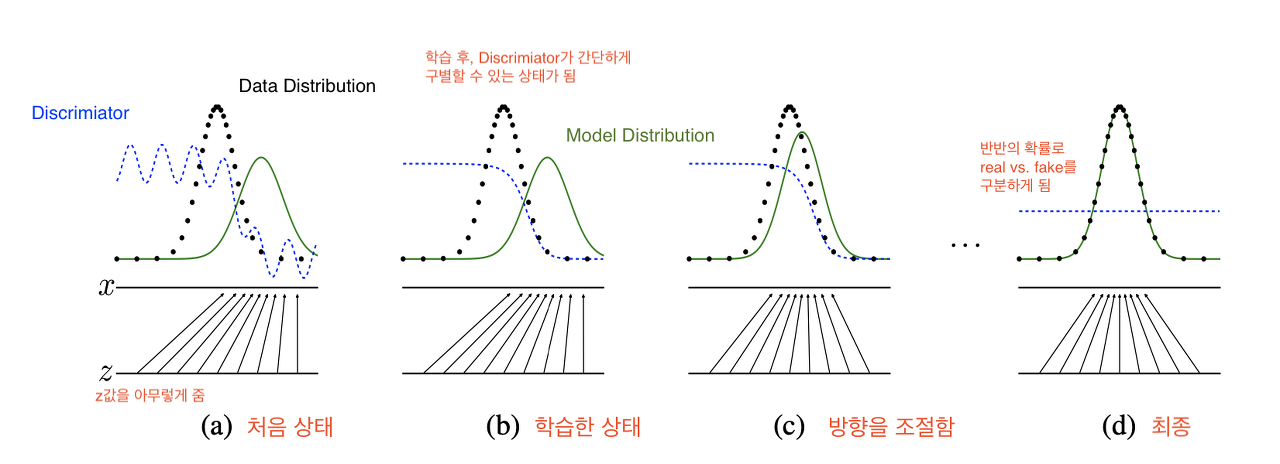
출처: https://wegonnamakeit.tistory.com/54 [WE GONNA MAKE IT]

결국 위조지폐범(Generator)은 구분하기 어려운 위조지폐를 만들게 된다. 경찰(Distriminator)은 이게 진짜인지 가짜인지 구별하기 가장 어려운 50% 확률에 수렴하게 된다.
파란 점선 --- : discriminator distribution (분류 분포) > 학습을 반복하다보면 가장 구분하기 어려운 구별 확률인 1/2 상태가 됨
녹색 선 ⎻ : generative distribution (가짜 데이터 분포)
검은색 점선 --- : data generating distribution (실제 데이터 분포)

확률적 생성모형

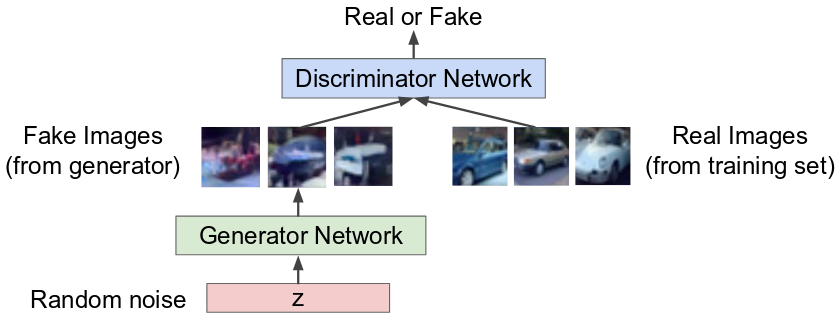
Generator 모델 : 랜덤 노이즈 벡터 또는 잠재변수를 입력받아 이미지를 만드는 업샘플링을 진행 데이터의 분포를 학습하는모델

G 모델 훈련과정은 D가 실수할 확률을 최대화 하는 것.

G는 훈련 데이터의 분포를 학습하여, 임의의 노이즈를 훈련 데이터와 같은 분포로 생성하고, D는 해당 인풋이 생성된 이미지인지, 훈련 데이터로 부터 나온 이미지인지에 대한 확률이 1/2가 되도록 한다.

Discriminator 모델 :

네트워크에 전달된 이미지가 실제인지 가짜인지를 판별
생성모델 G로부터가 아닌, 훈련 데이터로 부터 나왔을 확률을 추정하는 모델 -> loss

해당 대상을 그림을 그릴 수 있다는 의미

뉴럴 네트워크가 고양이와 개를 그리는 걸 배울(학습) 수 있다면, 반드시 분류도 할 수 있을 것이다.
즉, 피처(데이터 분포) 학습은 자연스럽게 따라온다.

Noise의 의미

GAN에서 Noise는 Auto Encoder의 Latent Variable이라고 할 수 있다.

Latent Variable

random noise 혹은 latent variable 불림(보통 논문에서 z로 사용)
- 사람마다 random noise 또는 latent variable 쓰는 이유는 의미에서 차이가 난다.
- random noise라고 쓰는 이유는 사전에 정의할 수 없음에 의미를 둔 표현쓰고,
- latent variable(잠재변수)은 autoencoder처럼 이것으로부터 출력 영상을 만들수 있기 때문에 이 표현를 쓴다.
Latent Variable은 직접적으로 관측되는 변수가 아니라, 측정변수(관측이 가능한 다른 변수)들로부터 추론이 가능한 변수이다.
여기서 이해가 안될 수 있지만, 관측이 가능한 다른변수(외부변수)는 cGan에서 yLabel를 의미하고 추론이 가능한 변수는 cGAN에서 random noise 또는 latent variable이라고 한다.
- 예를 들어, "건강"이라는 추상적인 변수는 직접적으로 측정할 수없는 "내재 변수"이지만, 몸이나 정신 상태를 표현하는 말로 자주 사용이다. 직접 계측할 방법은 없지만, 혈압, 맥박, 혈당, 체온, 체중, 허리둘레 등 "(많은) 관측이 가능한 외부 변수"로 부터 추론이 가능하다
- 이런 외부 변수로 부터 추상적인 건강이라는 내재변수를 도출하려면 수학적(알고리즘) 혹은 경험적(확률적) 모델이 필요하다.
- CNN를 예로 들면 입력 이미지를 컨브넷에 넣어지면 이미지의 크기는 작아지고 채널의 수는 늘어나는 추상화 과정이 일어난다 이 과정에서 해당 특성맵만으로는 어떤 이미지인지 알 수 없다. 하지만 이전에 이런 입력 이미지를 넣어 다는 것을 알아 해당 변수가 해당 입력 이미지를 나타낸다고 알 수 있다.
즉 latent variable에 이미지 생성에 관련된 condition을 부가하고, 이것을 통해서 이미지 생성을 가이드 할 수 있다면, 이제는 원하는 방향으로 이미지를 생성할 수 있게 된다.
일종의 차원축소 개념으로 해석하면 된다.

MiniMax Problem of GAN

The GAN Objective Function

${min_G max_DV(D,G) = \mathbb{E}_{x {\sim} p_{data}(x)}[logD(x)] + \mathbb{E}_{x {\sim} p_{z}(z)}[log(1-D(G(z)))]}$

${x}$: real 이미지
${z}$: latent code 또는 Random noise
${G(z)}$: fake 이미지
${D(x)}$: real 이미지라고 분류한 확률
${D(G(z))}$: D가 fake라고 분류한 확률
${p_{data}(x)}$: real 이미지 확률 분포
${p_{g}(G(z))}$: 가짜 이미지 확률 분포
${p_{z}(z)}$: Ramdom noise 확률 분포
${V(D, G) = log(D(x)), 0<= D(x) <=1}$

D should maximize V(D, G) : D 입장에서 V가 최댓값
1. D가 구분을 잘하는 경우, 만약 Real data가 들어오면
- D(x) = 1, D(G(z)) = 0
  : 진짜면 1, 가짜면 0을 내뱉음. (G(z)에 가짜가 들어온 경우, 가짜를 잘 구분한 것임)
- D의 입장에서는 minmaxV(D, G) = 0
- Maximize를 위해 V(D,G)을 0으로 보내는 게 D의 입장에서는 가장 좋음
G should minimize V(D, G) : G 입장에서 V가 최솟값
1. D가 구분을 못하는 경우, 만약 Real data가 들어오면
- D(G(z)) = 1
  : 가짜를 1로 생각함 (진짜를 구분하지 못하고 가짜를 진짜로 착각함)
- log 안의 D 값이 0이 되어, V 값이 -∞로 됨
- Minimize를 위해 V(D,G)을 -∞로 보내는 게 G 입장에서는 가장 좋음

def minimax_graph():
    plt.axvline(x=0, color='black', linewidth=1)
    plt.axhline(y=-0,color="black")
    plt.plot(np.arange(0.1,5,0.1),np.log(np.arange(0.1,5,0.1)),label='Discriminator')
    plt.plot(np.arange(-5,1,0.1),np.log(1-np.arange(-5,1,0.1)),label='Generator')

    plt.axvline(x=0.5, color='r', linewidth=1,label='0.5')
    plt.xlim([-5, 5])
    plt.ylim([-2,2])
    
    plt.legend()
    plt.show()

minimax_graph()

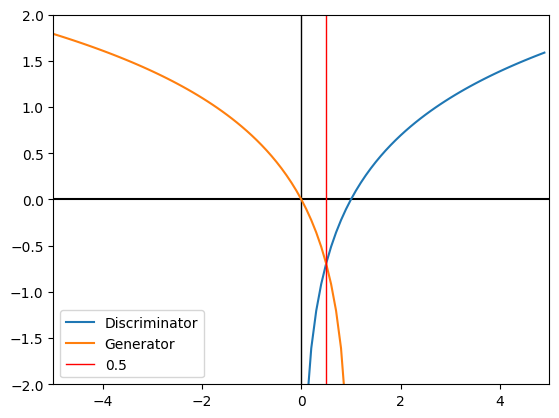
위의 minimax 그래프를 확인해 보면 D(x)에 대해서 x=1로 수렴하면 D(G(z)가 무한으로 발산하게 되고 반대로 D(G(z))에 대해서 z=0으로 수렴하면 D(x)가 무한으로 발산하게 된다.
그래서 두 함수가 절충할 수 있는 지점인 0.5확률(loss)에 수렴해야 된다.
여기서 0.5 즉 50%의 확률의 의미는 위조 지폐가 진짜와 구별되지 않는 다는 것을 의미한다.

Binary Cross Entrory

${BCE(x) = -{1\over N}\sum_{i=1}^N y_i log(h(x_i;\Theta)) + (1-y_i) log(1-h(x_i;\Theta)) }$

Theoretical Results

위에 정의한 minimax problem(최소 최대문제)가 실제로 풀 수 있는 문제인지 확인이 필요하다. 이를 위해, (1) 실제 정답이 있는지(existence)와 (2) 해가 존재한다면 유일한지(uniqueness) 검증이 필요하다.
1) Global Optimality: 실제 정답이 있는지(existence)
- GAN의 Minimax problem이 global optimality를 가지고 있다. Pdata(data distribution)이 generative model distribution이 정확히 일치할 때 global optimality이며 그때 global optimality(${P{g} = P_{data}}$)를 갖는가?

2) Convergence of Algorithm 1: 해가 존재한다면 유일한지
- 우리가 제안하는 알고리즘(discriminator: distribution model 학습하는 과정의 모델)이 실제로 global optimality(P_g = P_data)을 찾을 수 있는 가?

1. Global Optimality of $P_{g} = P_{d a t a}$

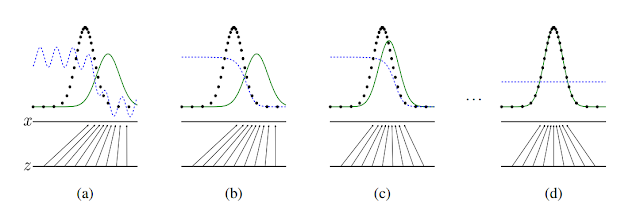
검은 점선: data_generating distribution
파란 점선: discrimitor distribution
녹샌 선: generative distribution
X선과 Z선: x=G(z)의 mapping을 보여줌.

(a): P_g 가 P_data와 전혀 다르게 생긴 것을 볼 수 있다.
(b): a상태에서 discriminator가 두 discribution(분포)을 구별하기 위해 학습을 하면 위의 그림처럼 smooth하고 잘 구별하는 distibution이 만들어진다.
(c): 이후 Generator가 discriminator가 구별하기 어려운 방향으로 학습하여 P_g가 P_data와 가까워지게 된다. G(z)가 x의 분포쪽으로 매핑되고 있다.
(d): 계속 학습시 결국 P_g = P_data가 되어 discriminator가 둘을 전혀 구별하지 못하는 즉, D(x) = 1/2인 상태가 된다.

1.1) Proposition 1.

G가 고정되었을때(trainable=false), 최적의 판별자 D는 다음과 같다.

**${D^*_G(x) = {P_{data}(x)\over {P_{data}(x) + P_g(x)}}}$**

어떠안 생성자 G가 주어졌을 때, 판별자 D를 위한 학습 기준은 $V (G, D)$ 를 최대화 하는 것( $m i n_{G} m a x_{D} V (G, D)$ )

${V(D,G)}$
${= \mathbb{E}_{x {\sim} p_{data}(x)}[logD(x)] + \mathbb{E}_{x {\sim} p_{z}(z)}[log(1-D(G(z)))]}$
${ = \int_x P_{data}(x) log(D(x))dx + \int_z P_z(z)log(1-D(G(z))dz}$
- D(g(z)) -> D(x) 근사
${ = \int_x P_{data}(x) log(D(x))dx + P_g(x)log(1-D(x))dx}$
${(a,b) \in \mathbb R^2 \setminus (0,0)이 아닌 실수 순서쌍 (a,b)에 대해}$
- a = P_data(x), b = P_g(x)
- ian_goodfellow 논문 gan의 a, b들의 확률은 0 또는 1로 구성되어 있다.
- alog(y) + blog(1-y)가 최대가 되어야 된다. 최대값을 구하기 위해 미분을 해서 기울기 가 0인 값을 찾아야 된다.
  - ${{a\over{y}} - {b\over{1 - y}} = 0}$
  - a(1-y) - by = 0
  - ${y = {a \over {a+b}} }$
  - $고 로 D_{G}^{*} (x) = \frac{P_{d a t a} (x)}{P_{d a t a} (x) + P_{g} (x)}$

결국 min_G max_D V(G,D)에서 안쪽의 max 문제부터 풀어주면 문제가 다음과 같다.

${C(G) }$
${ = max_D V(G,D) }$
${= \mathbb{E}_{x {\sim} p_{data}(x)}[logD(x)] + \mathbb{E}_{x {\sim} p_{z}(z)}[log(1-D(G(z)))]}$

${= \mathbb{E}_{x {\sim} p_{data}(x)}[logD^*_G(x)] + \mathbb{E}_{x {\sim} p_{g}(z)}[log(1-D^*_G(G(z)))]}$
${= \mathbb{E}_{x {\sim} p_{data}(x)}[ log {P_{data}(x)\over{P_{data}(x)+P_g(x)}} ] + \mathbb{E}_{x {\sim} p_{g}(z)}[ log {P_{g}(x)\over{P_{data}(x)+P_g(x)}} ]}$
${= \mathbb{E}_{x {\sim} p_{data}(x)}[ D_{KL}P_{data}(x)|| log {P_{data}(x)\over{P_{data}(x)+P_g(x)}} ] + \mathbb{E}_{x {\sim} p_{g}(x)}[ D_{KL}P_{g}(x)|| log {P_{g
}(x)\over{P_{data}(x)+P_g(x)}} ]}$

최적화 알고리즘

for epoch of training iterations do

for n_iter_D steps do -> Discriminator의 판별력이 더욱 강해진다.
- 배치 사이즈 m개의 noise 샘플 $z^{(1)}, z^{(2)}, . . . z^{(m)}$ 을 p_g(x)로 부터 추출
- 배치 사이즈 m개의 example(x) 샘플 $x^{(1)}, x^{(2)}, . . . x^{(m)}$ 을 p_data(x)로 부터 추출
- Distriminator 모델 업데이트 by gradient Descent
  - ${\nabla_{\theta}{1 \over m} \sum_{i=1}^m}[y_ilogD(x^{(i)})+{(1-y_i)}log(1-D(G(z^{(i)})))]$
  - G.trainable = false : Generator 모델은 학습이 되지 않는다.
  - D.trainable = true :
    - Discriminator 모델만 학습 된다.
    - 경찰이 위조범의 위조지폐를 구분하는 과정

end for -> Generator의 위조능력이 더욱 강해진다.
- 배치 사이즈 m개의 noise 샘플 $z^{(1)}, z^{(2)}, . . . z^{(m)}$ 을 p_g(x)로 부터 추출
- Distriminator 모델 업데이트 by gradient Descent
  - ${\nabla_{\theta}{1 \over m} \sum_{i=1}^m}[log(1-D(G(z^{(i)})))]$
  - G.trainable = true : Generator 모델은 학습만 학습한다.
  - D.trainable = false :
    - Discriminator 모델은 학습하지 않는다
    - 위조범이 경찰을 속이는 설정

end for

gradient-based update(경사 하강법)은 어떤 표준적인 gradient를 사용해도된다.
- 여기서는 momen-tum 경사 사용.
학습 계속 될수록 판별자는 판별능력이 더 강해지고 위조범은 위조능력이 더 강해진다.

DCGAN 구현

Deep Convolution GAN

import tensorflow as tf
from tensorflow.keras import models, layers
from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras

import argparse

class Data:
    def __init__(self, batch_size, z_input_dim):
        # load mnist dataset
        # 이미지는 보통 -1~1 사이의 값으로 normalization : generator의 outputlayer를 tanh로
        (x_train, y_train), (x_test, y_test) = mnist.load_data()
        self.x_data = ((x_train.astype('float32') - 127.5)/127.5)
        self.x_data = self.x_data.reshape( x_train.shape + (1,) )
        self.batch_size = batch_size
        self.z_input_dim = z_input_dim
        
    def get_real_sample(self):
        return self.x_data[np.random.randint(0, self.x_data.shape[0],size=self.batch_size)]
    
    def get_z_sample(self, sample_size):
        return np.random.uniform(-1.0,1.0,(sample_size,self.z_input_dim))

In [35]:

data = Data(2,z_input_dim=100)

In [36]:

test_real_data = data.get_real_sample()
test_z_data = data.get_z_sample(2)

In [37]:

print(test_real_data.shape)
print(test_z_data.shape)

(2, 28, 28, 1)
(2, 100)

In [49]:

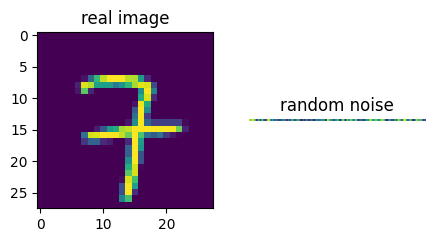
fig = plt.figure(figsize=(5,10))
fig.add_subplot(1, 2, 1)
plt.title('real image')
plt.imshow(test_real_data[0,:,:,0])
fig.add_subplot(1, 2, 2)
plt.title('random noise')
plt.axis('off')
plt.imshow(test_z_data[0:1])
plt.show()

class GAN:
    def __init__(self, learning_rate, z_input_dim):
        """
        D : Discriminator
        G : Generator
        GD : G+D, Generator 학습 모델
        """
        self.learning_rate = learning_rate
        self.z_input_dim = z_input_dim
        self.D = self.discriminator()
        self.G = self.generator()
        self.GD = self.combined()
        
    def discriminator(self):
        """
        진짜 이미지, fake 이미지 판별 모델
        """
        D = models.Sequential([
            layers.Conv2D(256,(5,5),padding="same",input_shape=(28,28,1),
                          kernel_initializer=keras.initializers.RandomNormal(stddev=0.02),
                         ),
            layers.LeakyReLU(0.2),
            layers.MaxPool2D((2, 2),strides=2),
            layers.Dropout(0.3),
            layers.Conv2D(512, (5,5), padding="same"),
            layers.LeakyReLU(0.2),
            layers.MaxPool2D((2, 2),strides=2),
            layers.Dropout(0.3),
            layers.Flatten(),
            layers.Dense(256),
            layers.LeakyReLU(0.2),
            layers.Dropout(0.3),
            layers.Dense(1,activation='sigmoid')
        ]
        )
        
        adam = keras.optimizers.Adam(learning_rate=self.learning_rate, beta_1=0.5)
        D.compile(loss='binary_crossentropy', optimizer=adam, metrics=['accuracy'])
        return D
    
    def generator(self):
        """
        fake 이미지 생성 모델
        """
        G = models.Sequential([
            layers.Dense(512, input_shape=(self.z_input_dim,)),
            layers.LeakyReLU(0.2),
            layers.Dense(128*7*7),
            layers.LeakyReLU(0.2),
            layers.BatchNormalization(),
            layers.Reshape((7,7,128)),
            layers.UpSampling2D(size=(2,2)),
            layers.Conv2D(64,(5,5),padding='same',activation='tanh'),
            layers.UpSampling2D(size=(2,2)),
            layers.Conv2D(1,(5,5),padding='same',activation='tanh') # -1~1
        ]
        )
        adam = keras.optimizers.Adam(learning_rate=self.learning_rate, beta_1=0.5)
        G.compile(loss='binary_crossentropy',optimizer=adam, metrics=['accuracy'])
        return G
        
    def combined(self):
        """
        Generator 와 Discriminator가 합쳐진 모델로, 
        Generator를 학습하기 위한 모델
        """
        G, D = self.G, self.D
        D.trainable = False
        GD = models.Sequential()
        GD.add(G)
        GD.add(D)
        
        adam = keras.optimizers.Adam(learning_rate=self.learning_rate, beta_1=0.5)
        GD.compile(loss='binary_crossentropy', optimizer=adam, metrics=['accuracy'])
        D.trainable = True
        return GD

In [34]:

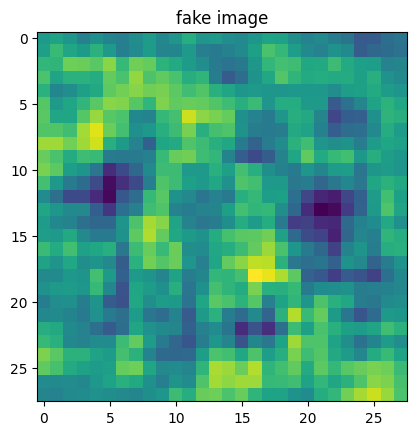
test_gan = GAN(0.001,100)

In [51]:

test_fake_iamge = test_gan.G.predict(test_z_data[0:1])

1/1 [==============================] - 0s 9ms/step

In [57]:

plt.imshow(np.squeeze(test_fake_iamge))
plt.title("fake image")
plt.show()

In [31]:

class Model:
    def __init__(self, batch, epochs, learning_rate, z_input_dim, n_iter_D, n_iter_G):
        self.epochs = epochs
        self.batch_size = batch_size
        self.learning_rate = learning_rate
        self.z_input_dim = z_input_dim
        self.data = Data(self.batch_size, self.z_input_dim)
        
        # D, G의 iter가 다른 이유: 
        # Generator는 Discriminator보다 더 많은 학습이 필요.
        self.n_iter_D = n_iter_D
        self.n_iter_G = n_iter_G
        self.gan = GAN(self.learning_rate,self.z_input_dim)
        
        # print status
        batch_count = self.data.x_data.shape[0] / self.batch_size
        print('Epochs:', self.epochs)
        print('Batch size:', self.batch_size)
        print('Batches per epoch:', batch_count)
        print('Learning rate:', self.learning_rate)
    
    def fit(self):
        self.d_loss = []
        self.g_loss = []
        for epoch in range(self.epochs):
            
            # train discriminator by real data
            dloss = 0
            for _ in range(self.n_iter_D):
                dloss = self.train_D()
            
            # train GD by generated fake data
            gloss = 0
            for _ in range(self.n_iter_G):
                gloss = self.train_G()
            
            # save loss data
            self.d_loss.append(dloss)
            self.g_loss.append(gloss)
            
            if epoch % 20 == 0:
                self.plot_generate_images(epoch, self.gan.G, examples=8)
                print('Epoch:', str(epoch))
                print('Discriminator loss:', str(dloss))
                print('Generator loss:', str(gloss))
            
        # show loss after train
        self.plot_loss_graph(self.g_loss, self.d_loss)
        
    def train_D(self):
        """
        Discriminator 학습
        """
        
        # Real data
        real = self.data.get_real_sample()
        
        # Generated data
        z = self.data.get_z_sample(self.batch_size)
        generated_images = self.gan.G.predict(z) # generator.trainable = False
        
        x = np.concatenate([real,generated_images],axis=0)
        y = np.array([0.9] * self.batch_size + [0] * self.batch_size)
        
        # train discriminator
        self.gan.D.trainable = True
        loss = self.gan.D.train_on_batch(x,y)
        return loss
    
    def train_G(self):
        """
        Generator 학습
        """
        
        # Generated data
        z = self.data.get_z_sample(self.batch_size)
        
        # labeling
        y = np.array([1]*self.batch_size)
        
        # train generator
        self.gan.D.trainable = False
        loss = self.gan.GD.train_on_batch(z,y)
        return loss
    
    def plot_loss_graph(self, g_loss, d_loss):
        """
        학습 loss 그래프 출력
        """
        
        # show loss graph
        plt.figure(figsize=(10, 8))
        plt.plot(d_loss, label='Discriminator loss')
        plt.plot(g_loss, label='Generator loss')
        plt.xlabel('Epoch')
        plt.ylabel('Loss')
        plt.legend()
        plt.show()
        
        
    def plot_generate_images(self, epoch, generator, examples=8):
        """
        생성된 mnist 이미지 출력
        """
        # plt info
        dim = (10, 10)
        figsize = (10, 10)

        # generate images
        z = self.data.get_z_sample(examples)
        generated_images = generator.predict(z)

        # show images
        plt.figure(figsize=figsize)
        for i in range(generated_images.shape[0]):
            plt.subplot(dim[0], dim[1], i + 1)
            plt.imshow(generated_images[i].reshape((28, 28)), interpolation='nearest', cmap='gray_r')
            plt.axis('off')
        plt.tight_layout()
        plt.show()

In [32]:

batch_size = 128
epochs = 1000
learning_rate = 0.0002
z_input_dim = 100
n_iter_D = 1
n_iter_G = 5

model = Model(batch_size,epochs,learning_rate,z_input_dim,n_iter_D,n_iter_G)

Epochs: 1000
Batch size: 128
Batches per epoch: 468.75
Learning rate: 0.0002

In [61]:

model.fit()

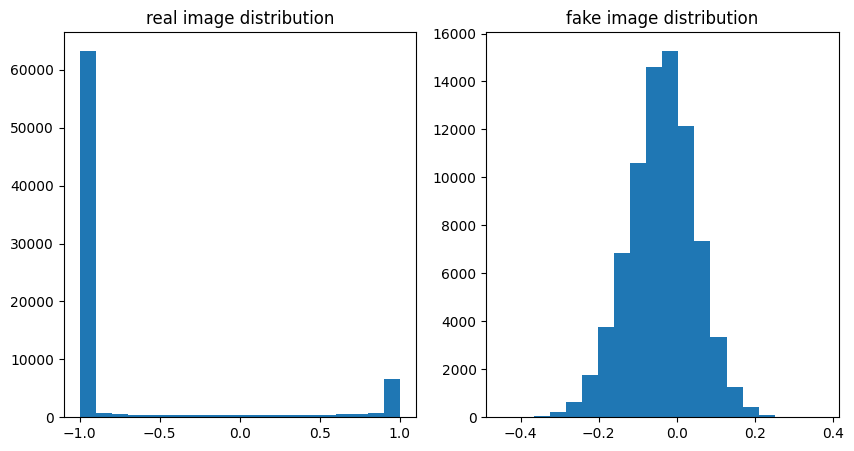
진짜 이미지 분포 와 학습 전 generator 분포 비교

plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title("real image distribution")
plt.hist(test_real_data.reshape((-1)),bins=10)
plt.subplot(1,2,2)
plt.title("fake image distribution")
plt.hist(test_gan.G.predict(test_z_data).reshape((-1)),bins=20)
plt.show()

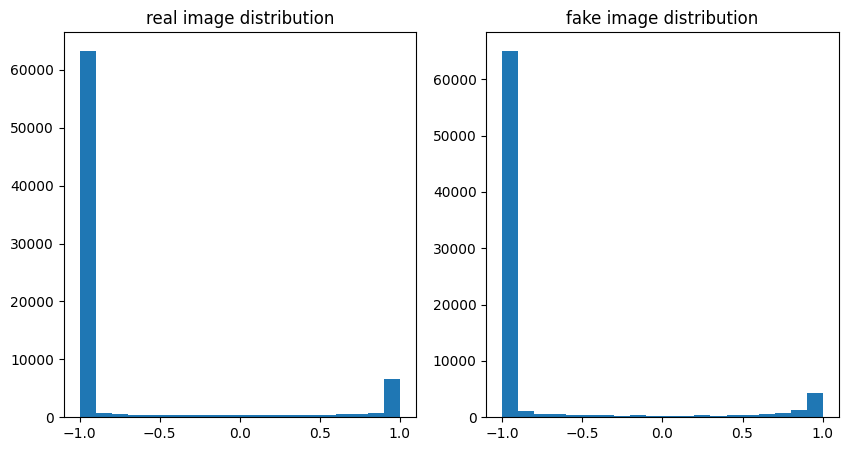
진짜 이미지 분포 와 학습 후 generator 분포 비교

plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title("real image distribution")
plt.hist(test_real_data.reshape((-1)),bins=20)
plt.subplot(1,2,2)
plt.title("fake image distribution")
plt.hist(model.gan.G.predict(test_z_data).reshape((-1)),bins=20)
plt.show()

'딥러닝' 카테고리의 다른 글

stanford dogs 분석 및 학습하기 (1)	2022.06.23
클래스 활성화의 히트맵 시각화 (0)	2022.06.23
컨브넷 필터 시각화 (0)	2022.06.23
Cat vs Dog 분류 모델 만들기 (0)	2022.06.18
Keras.1 Modeling (0)	2022.06.18

창민이 개발일지

GAN개념과 DCGAN 구현

생성적 적대 신경망(GAN)

적대적 생성

확률적 생성모형

해당 대상을 그림을 그릴 수 있다는 의미

Latent Variable

MiniMax Problem of GAN

Binary Cross Entrory

Theoretical Results

1. Global Optimality of $P_{g} = P_{d a t a}$

1.1) Proposition 1.

**${D^*_G(x) = {P_{data}(x)\over {P_{data}(x) + P_g(x)}}}$**

결국 min_G max_D V(G,D)에서 안쪽의 max 문제부터 풀어주면 문제가 다음과 같다.

최적화 알고리즘

DCGAN 구현

진짜 이미지 분포 와 학습 전 generator 분포 비교

진짜 이미지 분포 와 학습 후 generator 분포 비교

'딥러닝' 카테고리의 다른 글

티스토리툴바

GAN개념과 DCGAN 구현

생성적 적대 신경망(GAN)

적대적 생성

확률적 생성모형

해당 대상을 그림을 그릴 수 있다는 의미

Latent Variable

MiniMax Problem of GAN

Binary Cross Entrory

Theoretical Results

1. Global Optimality of Pg=PdataPg=Pdata

1.1) Proposition 1.

${D^*_G(x) = {P_{data}(x)\over {P_{data}(x) + P_g(x)}}}$

결국 min_G max_D V(G,D)에서 안쪽의 max 문제부터 풀어주면 문제가 다음과 같다.

최적화 알고리즘

DCGAN 구현

진짜 이미지 분포 와 학습 전 generator 분포 비교

진짜 이미지 분포 와 학습 후 generator 분포 비교

'딥러닝' 카테고리의 다른 글

관련글

티스토리툴바

1. Global Optimality of $P_{g} = P_{d a t a}$

**${D^*_G(x) = {P_{data}(x)\over {P_{data}(x) + P_g(x)}}}$**